昨晚我被一则新闻报道屏蔽了：北京时间4月10日晚9点，人类第一张黑洞照片正式发布。

看到这张照片，小吴极度震惊：爱因斯坦夫人太牛逼了！

同时，在看新闻的时候，小吴也注意到了一个细节。拍摄黑洞照片的事件视界望远镜于2017年开始拍摄黑洞，但直到2019年才公布。

我不禁想知道为什么拍黑洞的照片要花这么长时间。

于是我搜索了更详细的信息，找到了线索。其中一点就是望远镜观测到的数据量非常大！

2017年，8台望远镜的数据量达到10 PB (=10，240 TB)，2018年增加了格陵兰望远镜，数据量持续增加。庞大的数据量使得数据处理更加困难。

通常面试的时候，我总是说海量数据，海量数据。这一次，数据真的是海量数据。

数据流非常大，每个射电望远镜产生的数据只能通过硬盘存储。

所以现在问题来了。假设你是一个给黑洞拍照的研究员，给你一台内存有限的电脑。如何找出这些数据的中位数，或者判断某个数字是否存在？

1.找到中位数的大量数据

标题描述

现在有10亿个int数(在java中int占4B)和一台有1GB可用内存的机器。如何找出这10亿个数字的中位数？

中位数是有序列表中间的数字。如果列表长度为偶数，则中位数为中间两个数字的平均值。

主题分析

标题中有10亿个数字，每个数字在内存中占4B，因此需要10 * 10 8 * 4才能将这10亿个数字完全加载到内存中，大约需要4GB的存储空间。根据题目的限制，很明显所有的数字都无法加载到内存中。

在这里，我们可以在快速排序中找到基于二进制位比较和分割的中值，这实际上是桶排序的一个应用。

桶分类

假设这10亿个数字存储在一个大文件中，依次将一些文件读入内存(不超过内存限制：1GB)，用二进制表示每个数字，比较二进制的最高位(第32位)，如果数字的最高位为0，则将这个数字写入file_0文件；如果最高有效位为1，该数字将被写入file_1文件。

注意：最高位是符号位，表示file_1中的数字都是负数，而file_0中的数字都是正数。

通过此操作，10亿个数字被分成两个文件，假设file_0中有6亿个数字，file_1中有4亿个数字。

在这种划分之后，想一想：在哪个文档中寻找中位数？

10亿个数字的中位数是10亿个数字排序后的5亿。现在file_0中有6亿个正数，file_1中有4亿个负数。file_0中的数字大于file_1中的数字。排序后的5亿个数必须是正数，所以排序后的5亿个数必须位于file_0中。

也就是说，中位数在file_0中，是file_0中所有数字排序后的第1亿个数字。

现在，我们只需要处理file_0(不需要考虑file_1)。

对于file_0文件，可以采取同样的措施：将file_0文件的一部分依次读入内存(不超过内存限制：1GB)，用二进制表示每个数字，比较二进制的第二高位(第31位)，如果数字的第二高位为0，则写入file_0_0文件；如果下一个最高位是1，将其写入file_0_1。

现在假设file_0_0中有3亿个数字，file_0_1中有3亿个数字，中位数是file_0_0中的数字从小到大排序后的第1亿个数字。

放弃file_0_1，继续按照下一个最高位(第30位)划分file_0_0。假设file_0_0_0中有5000万个数字，file_0_0_1中有2.5亿个数字，中位数是file_0_0_1中所有数字排序后的数值。

2.判断海量数据中是否存在数字

标题描述

现在有10亿个int类型的数字(在java中int类型占4B)，一台有1GB可用内存的机器给出一个整数。如果你快速判断这个整数是否在10亿个数中？

主题分析

这里，可以使用布隆过滤器进行处理。

布隆过滤器是伯顿布隆在1970年提出的。

它实际上是一个长二进制向量和一系列随机映射函数。

它可以用来确定一个元素是否在集合中。它的优点是只需要占用很小的内存空间，查询效率高。

对于Bloom filter，其本质是一个位数组：位数组意味着数组的每个元素只占用1位，每个元素只能是0或1。

首先，布隆过滤器的位阵列中的所有位被初始化为0。例如，如果数组长度为m，则m位数组长度的所有位都被初始化为0。

0 0 0 0 0 0 0 0 0 0 0 0 1 。m-2 m-1

数组中的每一位都是二进制位。

除了一个位数组，Bloom filter还有k个散列函数。将元素添加到布隆过滤器时，将执行以下操作：

用k个散列函数计算元素值k次，得到k个散列值。根据得到的哈希值，将位数组中对应下标的值设置为1。

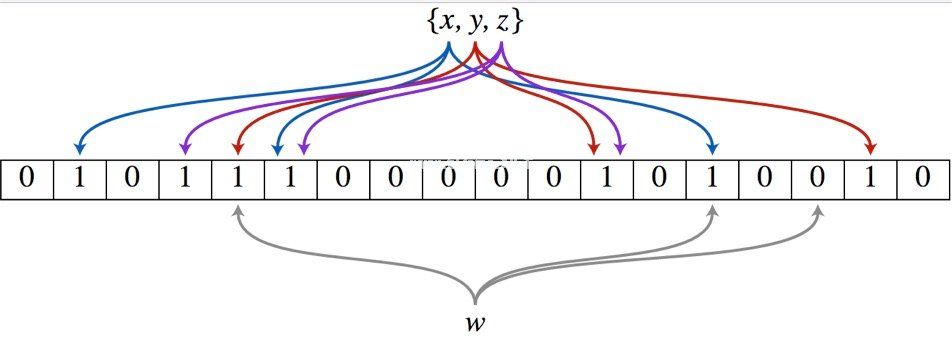
图1

例如，假设布隆过滤器有三个散列函数：f1、f2、f3和一个位数组arr。现在将2333插入布隆过滤器：

这些值被散列三次，得到三个值n1、n2和n3。将位数组中的三个元素arr [n1]、arr [N2]和arr [3]设置为1。

当判断一个值是否在Bloom过滤器中时，对元素进行三次哈希计算，然后判断位数组中的每个元素是否为1。如果所有值都是1，则表示该值在布隆过滤器中；如果存在1以外的值，则意味着元素不在布隆过滤器中。

花

摘要

以上是一些与边肖介绍的“黑洞照片”等海量数据相关的算法问题。希望对大家有帮助。如果你有任何问题，请给我留言，边肖会及时回复你。非常感谢您对我们网站的支持！如果你觉得这篇文章对你有帮助，请转载，请注明出处，谢谢！