推箱子，又称为“Box Push”，是一种经典的单人益智游戏，玩家需要将箱子推到指定的目标位置。随着游戏的普及，推箱子不仅在休闲娱乐中受到青睐，更成为了计算机科学研究的一个重要领域。本文将围绕推箱子自动求解算法进行详细阐述，并分享一些实用的应用技巧。

1. 推箱子的基本规则

推箱子的目标是将所有箱子推到预设的目标点上。尽管规则简单，但随着棋盘的复杂性和箱子的布局，游戏的求解难度会迅速上升。玩家只能推箱子，不能拉，也不能穿越障碍物。游戏的要素包括推箱子的数量、目标位置的布局以及玩家初始位置等。

2. 自动求解算法概述

为了解决推箱子问题，众多算法相继被提出。其中，最常见的有广度优先搜索（BFS）、深度优先搜索（DFS）、A*算法和Dijkstra算法等。这些算法通过不同的策略探索状态空间，寻找解决方案。

2.1 广度优先搜索（BFS）

BFS是一种无权图搜索算法，它适合于寻找最短路径。该算法从起始状态开始，逐层扩展所有可能的状态，直到找到目标状态为止。虽然BFS能够确保找到最优解，但在状态空间较大的情况下，内存消耗会极为严重。

2.2 深度优先搜索（DFS）

DFS则采取了一种更深的探索方式，优先访问较深的状态，其实现简单且占用内存较少。然而，DFS并不能保证找到最优解，也可能出现无限回溯的情况。

2.3 A*算法

A*算法结合了BFS和启发式搜索的优点，在搜索过程中考虑到路径代价和启发式评估，从而更有效地引导搜索方向。它使用启发函数来预测到目标的代价，通常能够更快找到最优解。

2.4 Dijkstra算法

Dijkstra算法适用于带权图的最短路径问题，它在每次选择的节点中都保证当前路径代价最小，但在复杂情况下同样会消耗大量时间和空间。

3. 算法的实际应用技巧

除了理解各种算法的实现方式，优化求解过程同样重要。以下是一些实用的应用技巧：

3.1 状态压缩

在推箱子的状态表示中，采取状态压缩的方式可以有效减少内存消耗。例如，可以将棋盘的状态用位运算表示，从而在存储和比较时更加高效。

3.2 剪枝策略

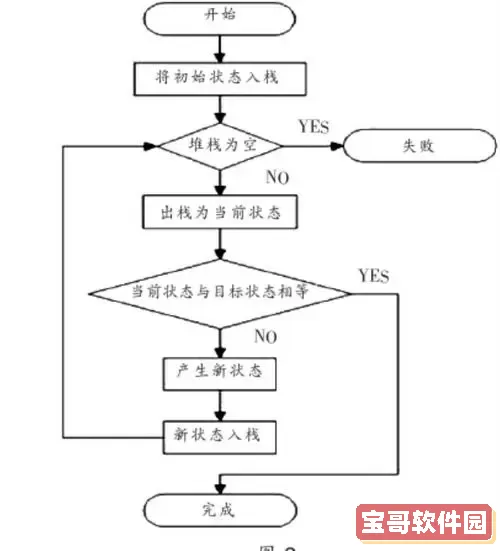
在搜索过程中，常常会出现重复状态或者无效状态。通过加入剪枝策略，可以在遍历状态树时即刻排除那些明显不可行的路径，从而减少不必要的计算。

3.3 启发函数的优化

对于A*算法来说，精选并优化启发函数能够极大提升搜索效率。设计启发函数时应考虑到推箱子的特点，例如使用曼哈顿距离来评估当前状态和目标状态的接近程度。

3.4 多线程处理

随着计算机技术的发展，多线程处理成为提升算法效率的一种有效方法。对于状态空间巨大的推箱子问题，可以采用多线程并行计算，从而加快求解速度。

4. 结论

推箱子作为一个经典的益智游戏，其自动求解算法的研究不仅丰富了计算机科学的算法领域，也为相关问题的解决提供了有效的方法。通过掌握基本的求解算法及其优化技巧，玩家和开发者可以在推箱子游戏中实现更高效的求解方案。

无论是一名爱好者，还是一位算法开发者，深入理解推箱子的求解机制，都能为你提供更广阔的思考空间，探索更多有趣的解决方案。